Face à face avec la symétrie 1/2
Sabine Rabourdin, Laboratoire S2HEP, EA4148, Université Claude Bernard Lyon 1
Sommaire des articles de ce dossier
Une comparaison entre physiciens indiens et français.
Résumé
Nous nous intéressons à la place de la symétrie dans la science à travers la question de son universalité. Pour cela, nous avons mené une série d’entretiens (70 en tout) semi-directifs avec des physiciens indiens et des physiciens français afin de déceler des éventuelles différences dans leur représentation du réel et de la science. Parmi les questions des entretiens, la symétrie avait une place de choix. Nous montrons les différences mais aussi les ressemblances entre les arguments des physiciens indiens et des physiciens français, concernant le rôle de la symétrie dans leur représentation du monde, et dans leur recherche. Nous proposons des pistes d’analyse pour expliquer le contexte culturel et historique, qui permet aux Indiens de mettre la symétrie au centre de leurs préoccupations. Nous émettrons aussi des hypothèses concernant le contexte culturel français. Au-delà de la question de la symétrie dans le cadre des sciences physiques, cet article est donc aussi une exploration de la non-symétrie culturelle, puisque nous mettons face à face des physiciens d’origines différentes, avec des particularités mais aussi des ressemblances. Si par « dissymétrie » nous nous permettons de signifier, non pas une absence totale de symétrie – qui serait alors une « asymétrie »- mais un manque de certains éléments de la symétrie, alors nous pouvons dire que nous avons mis à jour une dissymétrie culturelle dans le monde des physiciens.
Introduction
La science a été décrite comme une activité qui se démarque par des caractères spécifiques dont les plus partagés sont la rationalité et l’universalité : « L’activité scientifique vise à acquérir une connaissance fondée en raison, dont la portée soit universelle » (Coenen-Huther, 2002, p.221). Que la connaissance possède une portée universelle, cela semble un objectif louable. Mais peut-on penser que chaque humain – puisqu’il s’agit bien de ce groupe en guise d’universalité – appréhende une connaissance donnée de la même manière ? Pour tenter de répondre à cette question, nous nous sommes penchés sur la question de la symétrie, un principe dont la portée est a priori universelle, et à ses corollaires : dissymétrie et asymétrie. Ce texte s’intéresse donc à la place de la symétrie dans l’univers de la science à travers la question de son universalité.
Nous avons mené une série d’entretiens (70 en tout) semi-directifs avec des physiciens indiens et des physiciens français afin de déceler des éventuelles différences dans leur représentation du réel et de la science. Parmi les questions des entretiens, la symétrie avait une place de choix. Deux questions y faisaient référence, de manière directe, d’autres questions, de manière indirecte. Quelques différences notables sont apparues entre les groupes de physiciens français et indiens, à la fois qualitativement et quantitativement.
Nous allons développer cet article selon deux axes. Dans un premier temps, nous procéderons à une analyse des discours : quels sont les arguments des physiciens qui justifient leurs réponses à ces deux questions sur la place de la symétrie en science ? Nous montrerons les différences mais aussi les ressemblances entre les arguments des physiciens indiens et des physiciens français, concernant le rôle de la symétrie dans leur représentation du monde, et dans leur recherche. Dans un deuxième temps, nous proposerons des pistes d’analyse pour expliquer le contexte culturel, historique, qui permet aux Indiens de mettre la symétrie au centre de leurs préoccupations. Nous émettrons aussi des hypothèses concernant le contexte culturel français. Enfin, nous conclurons sur la portée de ces différences et de ces ressemblances.
Au delà de la question de la symétrie dans le contexte des sciences physiques, cet article est donc aussi une exploration de la dissymétrie culturelle, puisque nous mettons face à face des physiciens d’origines différentes, avec des particularités mais aussi des ressemblances.
I. Horizon de recherche
Peu d’études ont été faites dans l’analyse culturelle ou nationale des représentations de notions scientifiques, telles que la symétrie. Il faut déjà préciser ce que l’on entend par « culture » dans notre cadre d’analyse, car les notions d’ « identité » et de « culture » recouvrent plusieurs acceptions épistémologiques. « L’identité est une donnée complexe à appréhender, en raison à la fois de sa transversalité disciplinaire et des rapports dialectiques qui fondent les réseaux conceptuels auxquels elle peut être associée » (Férreol, Jucquois, 2004, p.155). Nous adhérons à la définition de la culture comme « un ensemble de schèmes interprétatifs qui permettent à chacun, au sein de ce cadre spécifique, de produire et de percevoir les significations sociales de ses propres comportements et de ceux d’autrui. » (Clanet, 1990, p.15) Les références pouvant servir de garde-fou dans le domaine de l’analyse culturelle des représentations scientifiques sont rares. « Plus souvent en effet, on s’est attaché à saisir l’émergence du neuf à l’échelle de petits groupes et non le maintien d’une tradition – jamais parfaitement stable- au sein d’un groupe très stable- et par là-même différencié. » (Pestre, 1984, p.4) Une des rares références est Dominique Pestre, qui, dans son livre Physique et physiciens en France de 1984, analyse les « spécificités nationales » des physiciens Français de l’entre-deux guerres. Il ne s’est pas à proprement parler intéressé par les représentations des physiciens, mais par les démarches d’enseignement et de recherche. Son approche est cependant novatrice car il se place en retrait par rapport à Gaston Bachelard et plus globalement à l’épistémologie française de son époque, pour qui, faire l’histoire des sciences c’était se centrer sur le « surrationalisme » des savants. Pestre estime que l’histoire des sciences doit se préoccuper des aspects non-rationnels des scientifiques. Au début du XXème siècle, Duhem avait déjà tenté de déceler des différences sensibles entre les physiciens anglais et des Français puis des Allemands, dans La théorie physique (1906). Marie-Jo Nye a également décrit des spécificités françaises dans l’organisation de la recherche en physique en France à la fin du XIXème siècle (Nye 1986). Jean Gayon a dressé un remarquable état des lieux des travaux sur la catégorie en histoire des sciences où il montre que les travaux sur les spécificités nationales sont rares, intéressants mais aussi délicats. En effet, cela impose de ne pas basculer dans des généralités ni des considérations identitaires. C’est pourquoi, lorsque les historiens s’appliquent à établir l’existence d’un style national dans tel ou tel secteur de la science, il s’agit surtout «d’identifier les traditions institutionnelles qui expliquent la persistance de styles ou stéréotypes nationaux de comportement scientifique » (Gayon, 1996). Mais l’exemple de Dominique Pestre montre que l’enjeu est valable. Celui-ci se revendique proche d’Alexandre Koyré, de Thomas Kühn, de Paul Forman, dans le sens où il estime que « l’objet de l’histoire des sciences est avant tout de démêler, dans ce que la science dit, dans les formes concrètes des énoncés qu’elle profère, les formes différentes de rationalité qui sont à l’œuvre, les représentations culturelles plus vastes qui les sous-tendent (les substructures psychologiques dirait Koyré), de façon générale les déterminations socio-mentales extérieures qui les marquent » (Pestre, 1984, p.6).
Dans tous les cas, ce genre de travaux montre que la pratique scientifique ne peut négliger les caractères propres à chaque pays. Notre travail va dans le même sens puisque nous allons montrer que des différences apparaissent entre les représentations des physiciens français et indiens.
La question de la symétrie est, quant à elle, un important sujet de travaux en philosophie des sciences, encore ouvert. La question qui nous intéresse au sein de ces travaux est celle du rapport entre les structures de l’expérience humaine et celles des lois fondamentales de la nature. Un incontournable ouvrage dans ce domaine est celui du physicien Joe Rosen (2008). Il nous propose par exemple de concevoir que « toute symétrie requiert une asymétrie » (p.8). Car « la symétrie requiert un cadre de référence, lequel est nécessairement asymétrique. L’absence d’une cadre de référence implique l’identité, et donc, l’impossibilité d’un changement, et donc l’inapplicabilité du concept de symétrie. » Rosen montre que la symétrie n’est possible qu’en fonction d’un environnement, d’un contexte. (Rosen, 2008, 9)[1].
Il est indiscutable que la physique a appuyé sa recherche des structures profondes du réel par la voie de la symétrie, mais elle l’a fait aussi à l’aide des brisures de symétrie. C’est une ambivalence qui montre que le langage est un façonnement de représentations, pour approcher le réel. La question de la symétrie reflète ainsi le façonnement mathématico- expérimental de notre appréhension du monde.
Soulignons enfin un travail notable sur la chiralité en anthropologie des sciences, mené par Arpita Roy, auprès des physiciens du CERN. En logeant au sein de la communauté de ces physiciens des particules, elle a observé comment les conceptions courantes de la matière, de l’énergie et de la lumière, découlent d’hypothèses sur la façon dont fonctionne l’univers. L’asymétrie de la latéralité lui a fourni un terrain étonnamment fertile pour interroger la prétention de la science sur le gouffre existant entre la pensée et la chose, le symbole et la réalité[2] (Roy, 2011). Malheureusement, ce remarquable travail ne s’intéresse pas aux spécificités culturelles de ces physiciens du CERN venant pourtant d’une grande diversité de pays. C’est donc au croisement de ces différentes démarches, dans un espace assez peu peuplé que se situe notre travail.
II. Recueil de données
La manière dont nous avons mené nos entretiens et sélectionné les physiciens est la suivante. Les entretiens auprès des physiciens indiens ont été menés en 2013 et 2014 au CERN à Genève, ainsi qu’en Inde, à Mumbaï et à Pune. Quelques entretiens ont été menés en France auprès de physiciens indiens en poste dans des laboratoires français. Les entretiens avec les physiciens français ont été menés dans différents laboratoires en région Rhône-Alpes et en région parisienne. Notre sélection s’est faite sur des critères de diversité des disciplines (physique théorique, physique expérimentale notamment), sur la diversité des classes d’âge et de genre. Nous avons cherché au plus près à retrouver la même diversité dans les deux échantillons. Nous ne revendiquons pas la représentativité de notre échantillon. Nous avons cependant pu remarquer que les caractères d’âge, de genre ou de discipline scientifique influaient très peu sur la réponse apportée à ces deux questions. Par ailleurs, l’ampleur de la différence entre Indiens et Français sur ces deux questions est telle qu’une influence culturelle est difficilement écartable. Nous avons aussi remarqué des ressemblances, et elles constituent également un objet d’analyse.
Les deux questions directes posées relativement à la symétrie sont :
– « Quel est, pour vous, l’aspect le plus important pour une théorie ? Autrement dit, parmi plusieurs théories proposant une description d’un ensemble de phénomènes, quels sont les aspects qui donneraient votre faveur à l’une d’elles ? »
Plusieurs aspects étaient suggérés, mais la question restait ouverte : beauté, simplicité, symétrie, compatibilité avec les faits expérimentaux, cohérence logique,…
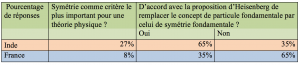
La symétrie apparût comme le premier critère pour 27% des chercheurs indiens, contre 8% pour les Français (cf.tableau 1). Il n’était pas donné de définition spécifique pour le mot « symétrie », ni pour les autres propositions (beauté, simplicité, etc.), permettant ainsi aux chercheurs de dévoiler le sens qu’ils lui attribuent.
– « Êtes-vous d’accord avec la proposition d’Heisenberg de remplacer le concept de particule fondamentale par celui de symétrie fondamentale ? »
La réponse fût positive pour 65% des chercheurs indiens, contre 35% pour les chercheurs français. Donc, une majorité d’Indiens se déclarait en accord avec cette proposition d’Heisenberg, alors qu’il s’agissait d’une minorité dans le cas des physiciens français (proportion inverse).
Rappelons qu’Heisenberg un physicien incontournable du XXème siècle qui a reçu le prix Nobel en 1932. Sa physique possède une dimension philosophique, notamment platonicienne. Comme l’explique Malcolm Longair, « au cœur de l’approche d’Heisenberg se trouvait le rôle joué par le comportement non commutatif des variables quantiques et la quantification du moment des variables spatiales. Pour s’en accommoder, un nouveau calcul mathématique a été inventé à partir du constat que les matrices suivaient précisément les règles algébriques correctes »[3](Longair, 2013, p. 278). Dans son autobiographie (1971), Heisenberg revendique une posture impopulaire de critique de la recherche en physique des particules et propose que la symétrie, et non pas les particules élémentaires, soit le point de départ d’une description du monde.
Tableau 1 : Pourcentage des réponses issues des entretiens (35 physiciens français, 35 physiciens indiens). Ce qui ressort des chiffres du tableau est que le concept de symétrie est bien plus important pour les physiciens indiens que pour les physiciens français. En effet, les physiciens indiens le jugent davantage nécessaire à la validité d’une théorie ; et davantage de physiciens indiens sont d’accord avec la proposition d’Heisenberg de remplacer le concept de particule fondamentale par celui de symétrie fondamentale.
III. Analyse des discours
III. A. Discours des physiciens indiens
III. A. 1. Les théories modernes en physique font appel au concept de symétrie
L’un des arguments au sujet de l’importance du concept de symétrie mis en avant par les physiciens indiens est sa présence essentielle dans les nouvelles théories de la physique moderne. Un théoricien spécialisé en gravité quantique de l’Inter-University Center for Astronomy and Astrophysics (IUCAA), à Pune, explique que « la particule n’est plus un concept fondamental tel qu’il a pu l’être à l’époque d’Heisenberg. Aujourd’hui, nous avons des concepts plus basiques, appelés les cordes qui sont, bien-sûrs, dirigés par la symétrie. Donc, Heisenberg avait raison de dire que c’est la symétrie qui conduirait à une meilleure compréhension de la nature de la matière. »[4]
Une expérimentatrice en physique nucléaire du TIFR indique : « Je suis d’accord avec Heisenberg parce que je sais que le comportement des particules peut seulement être décrit par la mécanique quantique qui est basée sur la symétrie. »[5] Une expérimentatrice d’un tout autre domaine, la physique des hautes énergies, indique que son domaine de recherche est basé sur l’idée de symétrie. « Dès que vous trouvez une symétrie, les choses sont plus simples. Je ne sais pas exactement ce que serait le remplacement du concept de particule fondamentale par celui de symétrie, il est possible que nous apprenions à partir des symétries fondamentales telles que nous l’espérons dans les dix prochaines années, avec les nouvelles avancées de la super-symétrie. Il s’agit d’une symétrie additionnelle. D’autres symétries doivent se trouver là. »[6] Pour un éminent théoricien du TIFR, la symétrie est le principe qui le guide le plus dans ses recherches parce que, pour lui, « les lois les plus fondamentales de la physique, les lois de conservation, sont une propriété émergente de la symétrie ». Ce premier argument est donc fondé sur l’usage courant des symétries dans les théories modernes de la physique.
III. A. 2. La symétrie est dans la nature
Un autre argument est basé sur la conviction que la nature est symétrique. Un physicien indien de la matière condensée est à ce point persuadé que « la symétrie est dans la nature », qu’il présume que l’ensemble des physiciens est de cet avis. « Il existe une forme d’ordre mathématique, de symétrie partout », dit-il. « Pourquoi sommes-nous tous symétriques ? ». Cet argument est repris par trois jeunes post-doctorants indiens en physique des hautes énergies au TIFR : « De toute façon, la symétrie est dans la nature. » conviennent-t-ils. L’aspect le plus important d’une théorie, explique une physicienne, est la symétrie parce que « la plupart des choses sont symétriques dans le monde ». Alors, si la symétrie est partout, comment réagissent ces chercheurs face à des asymétries manifestes, telles que l’écoulement du temps ou les phénomènes chaotiques ? Le temps est censé être symétrique en physique quantique. Mais pas en thermodynamique. « C’est troublant que le temps ne soit pas symétrique » s’interroge l’un d’eux. Certains vont alors estimer que le temps est symétrique dans certaines théories : « La flèche du temps est une propriété émergente dépendante de l’échelle et de la théorie utilisée : la thermodynamique, par exemple ou la cosmologie, n’utilisent pas la même flèche du temps. »[7]. Certains estiment que l’asymétrie révèle une symétrie « intérieure ». « Une belle équation est comme une musique : elle possède une symétrie intérieure. Elle assemble des différences, comme un puzzle. » estime un chercheur en physique statistique de la matière condensée. Une physicienne estime qu’au fond, « même quand il existe des brisures de symétries, originellement, il y avait une symétrie. »[8] Une réponse face à l’absence de symétrie de la flèche du temps ou de phénomènes chaotiques – est que ces phénomènes répondent toutefois à un ordre, à un équilibre. Même les évènements chaotiques peuvent correspondre à un ordre, à un équilibre, comme le témoigne un physicien théoricien. En fait cette question de la symétrie semble liée dans l’esprit d’un grand nombre de physiciens indiens à la beauté. « J’aime l’art, j’aime la symétrie mais pas trop, sinon c’est ennuyeux. Quand vous allez à un musée, et que vous voyez une chose complètement symétrique, cela garde votre attention un moment, mais… »[9] fait remarquer un autre. « La beauté c’est la symétrie, ou une asymétrie : une symétrie brisée de manière harmonieuse ». Il nous a donc semblé qu’il pouvait y avoir une relation entre cette question de la symétrie, et une question posée aussi lors des entretiens, à savoir : « La nature ou la réalité vous paraît-elle ordonnée ou chaotique » ? En croisant les réponses, il apparaît qu’en majorité, ceux qui sont d’accord avec l’importance de la symétrie sont les mêmes que ceux qui perçoivent la nature ordonnée.
III. A. 3. La symétrie renvoie à l’ordre dans la nature
| Pourcentage de réponses | Nature ordonnée | Nature chaotique | Les deux | |
| Inde |
0,57 |
0,13 |
0,30 |
|
| France |
0,44 |
0,21 |
0,35 |
|
Tableau 2 : Pourcentage de réponses apportées à la question : « La nature vous paraît-elle ordonnée ou chaotique » ?
Même si les réponses entre chercheurs indiens et français ne sont pas autant opposés que dans les deux questions sur la symétrie, une différence forte apparaît quand même, puisque 57% des Indiens trouvent la nature ordonnée, tandis que 44% des Français sont de cet avis. Il nous a semblé intéressant de vérifier si ceux qui répondaient sans hésiter « ordonné » étaient les mêmes que ceux qui accordaient de l’importance à la symétrie. Il s’avère qu’il existe manifestement un lien entre répondre « ordonné » et répondre positivement à l’importance de la symétrie. Ainsi, 81% des Français qui répondent que la nature est ordonnée accordent une importance à la symétrie et c’est aussi vrai pour 85% des Indiens. Donc, il existe un lien fort entre l’importance accordée à la symétrie dans les théories physiques, ainsi que dans le choix de représentation, et la perception que la nature/réalité est ordonnée.
“Pour moi, le chaos est équilibré. Dans le sens où le chaos est aussi une loi de la nature. Je crois qu’il y a de l’harmonie dans la nature »[10] révèle un physicien indien. Un autre explique : « La nature est certes parfois chaotique, mais le chaos est aussi une forme d’ordre. » D’autres encore : « Je crois qu’il y a un ordre caché auquel nous devons nous adapter”, “Je suis fasciné par les structures que développe la nature[11]».
Même si la majorité des physiciens indiens conçoit la réalité comme étant ordonnée, il en reste qui laissent une place au chaos (ceux qui sont dans la case « les deux »). Dans ce cas, l’ordre apparaît comme un phénomène émergent du désordre. « La nature est chaotique, l’ordre est un phénomène émergent » explique un physicien indien. Pour un autre : « Si vous regardez les choses, vous voyez de l’ordre. Par exemple, dans une table, les électrons sont chaotiques. Du dehors, vous voyez une apparence d’ordre »[12]. Un physicien a fait une conférence grand public sur la symétrie en physique et y explique que la causalité est le principe sous-jacent des idéalisations scientifiques[13] : « Je dois vous révéler ma philosophie : j’ai le sentiment que l’esprit humain est séparé entre l’analyse probabiliste du chaos, et l’ordre causal du monde ».
Ce que nous pouvons conclure des discours des physiciens indiens au sujet de l’idée de symétrie, c’est que le monde leur paraît majoritairement symétrique, même quand il prend des apparences de dissymétrie, comme avec la flèche du temps. Et l’idée d’une nature ordonnée n’est pas indépendante de cette importance accordée à la symétrie.
III. A. 4. Jongler avec la symétrie et la particule, selon l’échelle d’observation
Concernant la proposition d’Heisenberg, certains physiciens indiens optent pour la symétrie au détriment de la particule parce que, d’après eux, la particule fondamentale n’existe pas. L’histoire de la physique leur a montré que lorsque l’on trouvait une particule que l’on croyait fondamentale, on se rendait compte qu’elle était elle-même composite. Les candidats les plus récents au titre de “particules fondamentales” sont les “quarks” constituants des hadrons, qui n’ont pourtant pas été observés en tant que tels. Un physicien théoricien du TIFR raconte : « Geoffray Chew, avec sa théorie du Boostrap[14] dans les années 70, a repris l’idée d’Heisenberg d’abandonner l’idée de particule élémentaire. Il ouvrait les portes de ce qui était connu en philosophie orientale, à savoir qu’il n’y a rien de fondamental. A son époque, les chercheurs commençaient à faire des expériences avec des particules en percutant par exemple des protons ensemble, et observaient des phénomènes de dispersion. De quoi s’agissait-il ? De protons, de neutrons ? Ils parlaient de hadrons, parce qu’ils ne comprenaient pas ce à quoi ils avaient à faire. Les hadrons donnaient naissance à quelque chose d’autre. L’idée de particule élémentaire s’envola. Je pense que cela a des implications philosophiques profondes. Ce que l’histoire du modèle standard a montré c’est que nous ne sommes probablement pas prêts à faire de la physique à ce niveau de complexité parce que nous pensons encore de manière très étroite »[15].
Un certain nombre de physiciens optent pour l’utilisation des deux concepts, la symétrie et la particule, en fonction du niveau auquel on se situe. Il s’agit d’une forme de relativisme. Un cosmologiste estime que « Beaucoup de choses fonctionnent bien avec le concept de particule fondamentale, mais lorsque vous allez à un niveau très profond, alors l’idée de symétrie devient importante, nous essayons de considérer des dispositifs pour comprendre les aspects multidimensionnels d’un problème. Donc, je ne vois pas pourquoi il faudrait choisir une chose au détriment d’une autre. A un certain niveau, quand ça devient complexe et multidimensionnel, alors les mathématiciens arrivent, et ils apportent cette notion de super-symétrie, et je crois que cela à aide à résoudre les équations. En vous-même, qu’essayez vous de comprendre ? Si vous êtes heureux en essayant d’expliquer quelque chose. Par exemple, vous utilisez une pile à électrolyse. Et si vous voulez utiliser le soleil, vous êtes face à un problème différent, n’est-ce pas ? Alors, vous devez inventer de nouveaux outils, de nouvelles notions »[16].
L’idée est de prendre ce qui fonctionne, en fonction du contexte et des besoins. Ainsi, un astrophysicien du TIFR explique simplement qu’il a pu constater qu’utiliser la symétrie fonctionnait dans ses recherches. Et il la considérera comme un élément important tant que ca continuera à fonctionner. Les comportements et les lois de la matière sont très différents à basse ou à haute énergie. « Nous pouvons utiliser les deux concepts, explique un autre théoricien en en physique de la superconductivité : symétrie et particule. Je suppose qu’Heisenberg parlait du modèle standard. Donc, oui, la symétrie semble importante. Pour nous aussi, la symétrie est un aspect important. Nous l’utilisons sans arrêt, pour construire des modèles de réseau cristallin. Pas toujours, il arrive que ce ne soit pas symétrique. » [17] Une éminente physicienne de Bangalore en physique des particules, estime qu’elle pourrait être d’accord avec le fait de remplacer le concept de particule fondamentale par celui de symétrie fondamentale mais pas pour toutes les particules, seulement pour les particules reliées à des forces ». Il s’agit donc d’utiliser les concepts de manière contextuelle. Ce qu’exprime ce physicien indien : « On n’est pas obligé de se passer du modèle des particules pour avoir de la symétrie. Ils ne sont pas relies à la même chose. C’est une question de point de vue tout cela »[18].
L’un des chercheurs interrogés, théoricien de la supergravité, celui qui a fait un exposé grand public sur le concept de symétrie en physique estime que la symétrie permet de déduire un tout d’une partie, elle rend possible l’atomisme, le réductionnisme. C’est donc un outil essentiel des sciences. Elle permet de rendre les lois de la physique possibles : « un atome d’hydrogène à Mumbaï est le même qu’à Paris ».
Figure 1. Extrait visuel de la conférence de A.D, 2004. Sans symétrie, on ne peut déduire le tout à partir d’une partie. Exemple avec les piliers du Parthénon.
Et pourtant, dit-il lors de l’entretien, c’est dépassé, qui sait, la théorie fondamentale n’est peut-être pas particulièrement symétrique ? La symétrie existe dans le monde quotidien à notre niveau. Mais au-delà ? » [19].
Le choix du concept est donc adapté au contexte et au niveau d’échelle que l’on étudie. Il n’y a donc pas de concept absolu de prédilection. Un physicien des particules estime ainsi que « ce n’est pas parce que c’est un concept mental que ce n’est pas une réalité. Il ne s’agit pas de basculer dans l’extrême inverse non plus. Il y a équilibre entre les deux versants, il existe une dualité. On peut opter pour vision duelle, particulaire et mathématique, symétrique » [20].
III. A. 5. Manque de confiance : je dis « oui » car je ne sais pas
Il ne faut pas écarter l’hypothèse qu’une partie des physiciens indiens acquiescent à la proposition d’Heisenberg, pour des raisons de respect dû à l’autorité, ou du fait d’une sous-estime personnelle. «Je ne suis personne pour me prononcer »[21] furent-ils plusieurs à répliquer, tout en acceptant finalement de se prononcer. D’après un philosophe des sciences indien interrogé, anciennement physicien, « peut-être que les physiciens n’ont pas compris la question. Ils ont juste dit « oui » parce qu’Heisenberg est quelqu’un de célèbre et doit donc avoir raison. Ils ont un problème de confiance en eux. Les Français n’ont pas ce problème »[22]. Il est incontestable qu’il y a une différence sur l’attitude vis-à-vis d’Heisenberg et de la liberté prise pour le critiquer. Des physiciens Français par exemple n’hésitent pas à dire : « Il s’est trompé sur pas mal de choses, mais les gens n’ont pas osé s’opposer à lui ». « Heisenberg n’a pas dit que des trucs bien ! ». Les discours des physiciens indiens ne sont pas aussi critiques. L’un d’eux dit à propos d’Heisenberg : “C’est un très grand homme, c’est une très grande déclaration. Je ne suis pas versé dans tout cela. » Cependant il ajoute : « mais j’ai été un observateur de la physique des particules. […]C’est probablement vrai »[23]. Il fait donc appel à son expérience pour conclure sur la valeur de cette proposition d’Heisenberg, et pas seulement sur le statut de ce personnage. Il est possible que le respect traditionnel pour l’autorité ou le manque d’estime induisent une tendance dans les réponses, cependant, nous avons pu voir plus haut que l’accord exprimé avec Heisenberg était très souvent appuyé par des arguments élaborés. Donc, cette hypothèse devrait assez peu influencer l’adhésion majoritaire envers la symétrie.
Notre impression est que l’accord avec la proposition d’Heisenberg repose à la fois sur le respect d’une figure qui fait autorité dans le domaine, ainsi que sur l’accord avec sa proposition de prioriser la symétrie. La première raison est cependant moins présente que la seconde dans les réponses des physiciens.
III. A.6. Ceux qui ne sont pas d’accord
La minorité des physiciens indiens qui ne sont pas d’accord avec la proposition d’Heisenberg de remplacer le concept de particule par celui de symétrie se justifie par des raisons de deux ordres :
– la particule leur plaît. Ainsi un physicien théoricien de Mumbaï aime voir le monde de manière particulaire. « J’aime la manière dont je m’intéresse au monde autour de moi. Et ce que je vois ce sont des particules. J’aime l’idée de particule. Je ne sais pas ce que cela veut dire. Nous savons que ce sont des fluctuations quantiques des champs »[24] ;
– la symétrie est trop restrictive, ils préféraient un autre concept, plus fondamental. « La symétrie est trop restrictive, j’opterai plutôt pour le dynamisme, l’émergence ».
En conclusion de cette partie sur l’analyse du discours des Indiens, et avant de passer aux Français, nous pouvons caractériser ces discours par :
– Le respect des figures qui font autorité dans la science
– L’importance de l’ordre et de la symétrie dans leur représentation de ce qu’est la réalité ou la nature
– Le choix d’utiliser des concepts qui fonctionnent, en fonction des domaines d’utilisation
[1] Rosen s’appuie sur un exemple : « Considérons par exemple un triangle équilatéral. Son apparence est immune d’une rotation par 120°C à partir de son centre dans son plan. Mais quel est ce changement que nous appelons « rotation par 120° » ? Faîtes ce que vous voulez au triangle, pivotez le, étirez-le, tordez-le, le concept de rotation est inapproprié à moins que nous ayons un cadre de référence qui puisent révéler les changements. La situation totale, celle du triangle équilatéral couplée avec son environnement, possède par contre des aspects qui ne sont pas indemnes sous une rotation de 120°. Les murs de la pièce, par exemple, pourraient servir du cadre de référence, puisqu’ils sont asymétriques sous 120° de rotation. Ainsi, le triangle équilatéral est symétrique dans le contexte de son environnement. »
Texte original en anglais :“A way of expressing the relation between symmetry and asymmetry is this : “symmetry requires a reference frame, which is necessarily asymmetric. The absence of a reference frame implies identity, hence no possibility of change, and hence the inapplicability of the concept of symmetry. Consider, for exemple, a equilateral triangle. Its appearance is an aspect of it that is immune to 120°rotation about its center in its plane, so it possesses symmetry under 120 ° rotations with respect to appearance. Or so we might blithely think. But what is this change we call “120° rotation” ? Do what we will to the triangle –twist it, twirl it, twitch it, swivel it, when it rotated by 120, or rotated at all for that matter ? […]The total situation that of the equilateral triangle together with its environment does possess aspects that are not immune to 120◦ rotation and that can thereby serve as a reference frame for 120◦ rotation. The walls of the room, for instance, could serve as reference frame, since they are asymmetric under 120◦ rotation. Thus, rotation by 120◦ is indeed a change. The equilateral triangle is symmetric in the context of its environment. It is symmetric under 120◦ rotation thanks to its environment’s lack of immunity to 120◦ rotation, thanks to the asymmetry of the total situation – triangle plus environment – under the rotation.» (Rosen, 2008, 9)
[2] « Ainsi, les lois de la physique traitent différemment les objets de latéralité asymétrique contraire : une différence (chiralité), initialement formulée dans la théorie, est transformée en une asymétrie observée expérimentalement (violation de la parité). Pour les particules sans masse, hélicité et chiralité sont définis comme étant intrinsèque, alors que pour les particules de masse, l’hélicité est un attribut relationnel. Ce mouvement est lui-même autorisé lorsque les aspects relationnels sont traités comme «relativiste», en impliquant la présence d’un observateur ou d’un cadre de référence, ce qui du point de vue de la physique moderne pourrait être isolé comme un ensemble de règles et d’horloges » (Roy, 2011, p.74) traduction personnelle de l’anglais vers le français.
[3] “At the heart of Heisenberg’s approach was the fundamental role played by the non-commutative behaviour of the quantum variables and the quantization of both the momentum and spatial variables. To accommodate the features, a new mathematical calculus had been invented from the realization that matrices followed precisely the correct algebraic rules.”
[4] « Well, yes, particle is no longer a fundamental concept as it was in Heisenberg’s time. Today we have more basic concept called string which is of course driven by symmetry and so Heisenberg was right that it is the symmetry that has led to deeper understanding in the nature of matter. »
[5] V.N. 4.17 “Yes I agree with Heinsenberg I know the behavior of particles can only be described through quantum mechanics which is based on symmetry.”
[6] K.M. 25 High energy physics is based on the idea of symmetry. Once you found a symmetry, things are more simple.
33.4. Yes, I would say because symmetry we see that it really plays a very important role in many aspect. I don’t really know exactly what will be the replacement of fundamental particle by fundamental symmetry, but it is possible that we learn from fundamental symmetry like we are hopping in next 10 years new from super-symmetry. It is additional symmetry. Some other symmetry may be there.
[7] “Arrow of time is an emergent property depending on the scale/theory, physical law for exemple thermodynamics, or cosmological, give different arrow of time.”
[8] because most of things are symmetric in the world and even when there are some cracks, then originally there is symmetry.
[9] “I love arts so I love symmetry but not too much, otherwise it is boring. When you go to museum and you see a completely symmetrical things, it keeps your attention for a while, but. ..”
[10] « For me, chaos is balanced. In the sense that nature is dictated by law of nature, chaos is also law of nature. I don’t believe in laws, I think there is harmony in nature”.
[11] “I am amazed by the structures that are developed by nature. It looks like there is lot of order, even the chaotic behavior is probably intended for a certain purpose.”
[12] “If you look at things you see there is order. for exemple in a table electrons are chaotic, from outside you give this property of a table. It is an emergent phenomenon.”
[13] Scientific Idealizations: Psychology and Metaphysics ASET Colloquium, TIFR, February 8, 2008
[14] Selon la théorie boostrap, en effet, la nature ne peut pas être réduite à des entités fondamentales, mais doit être envisagée de manière complémentaire. C’est-à-dire en termes de relations communes.
[15] “Geoffray Chew (bootstrap theory) took former Heisenberg’s idea that we should give up the idea of elementary particle. He was bringing heavy doors of what is known as eastern philosophy to say basically there is nothing fundamental. What was happening at that time people beginning to do experiments with particles they hit protons together scattering experiments.
G Chew was saying more fundamentally is it a proton, is it a byon is it a neutron ? Because they did not understandThey were talking of hadrons. Each hadron was giving rise to something else. The idea of elementary particle went away. I think It has profound philosophical applications. What the history standard model has shown we are probably not ready to do physics for that level of complexity because we are still thinking very narrow.”
[16] “Lot of things work quite well when you mean fundamental particle, but when you go down to very deep level, then the ideas of symmetry and all, we try to consider mathematical devices to understand multidimensional aspect of a problem, then you need that, ok. So I don’t know why you have to choose one thing or the other. Because at some level, everything you do everything you need you think you really understand what particle is. But when you go down, to understand super-symmetry and all that you know at the quark level and other things, when it becomes complex and multidimensional, then mathematician come in, and they bring this notion of super-symmetry and I think it helps to solve equations.
In your self what are you trying to understand ? If you are happy with explaining something. For exemple, you use a battery, the power for electrolyze and atoms, you design a new battery with students, and then you go to sun and then you have a different problem right ? So then you have to invent new tools, new notions. So I think you have bring new things, to break, to understand and explain.”
[17] We can use both concepts : symmetry and particle. I guess Heisenberg was talking about the standard model. So yes symmetry seems important. And for us, two, symmetry is an important aspect. We use it always, to construct lattice models, not always, sometimes it is not symmetric.
[18] They are not in contradiction with each other, you don’t have to choose one. It is a view point.
[19] G.M. 38.18 These are old doctrines. Who knows maybe the fundamental theory is not particularly symmetric, I think the fundamental theories are not particularly symmetric. It maybe quite ugly from the point of view of symmetry. But symmetry eventually do exist in the current world at our scale. Certainly gauge symmetry is a very important thing. It is like a carry principle for standard modal that has been discovered by insisting on gauge symmetry. Certainly it is like that. But I wouldn’t engage myself on symmetry.
[20] “It is the viewpoint of a mathematical physicist. I don’t say there is no truth in it. Or not substance in it. There is a substance in it. But physical reality has some importance. But too much of mathematization I am a little skeptical of that, because it takes away the reality which you can see within your range. It strikes me on my head. Particle reality was a mental reality. There is lot of conclusion there. They say that ho It is a mental concept therefore it is not reality, but it is not like that. Extreme position is opposite. There is an interplay in the two side, there is a duality.”
[21]“ I am no one to agree or disagree with that ?”
[22] “Maybe Indian physicist did not understand the question. They just said yes because Heisenberg is famous and he must be right. There is a problem of self-confidence. French don’t have this problem.”
[23] “That is very big man. That is a very big statement. I am not so clouded in all these things. But I have been sort of observer of particle physics because we don’t do that with other thing that basic knowledge. It is probably true, I believe, it’s probably true.”
[24] « I like the way I am interested in what is happening around me. What I see is particle. I like the idea of particle. I don’t know what it means. We know that particles are quantum fluctuations of fields.”