Emotion esthétique et économie mathématique
Le rôle de l’émotion esthétique dans la construction de l’économie mathématique
Emmanuel Petit est professeur de Sciences Économiques à l’Université de Bordeaux et membre du GREThA (UMR CNRS 5113).
Résumé
Cet article porte sur le rôle épistémique des émotions esthétiques en économie mathématique. Nous formons l’hypothèse que la formalisation mathématique en économie a contribué à façonner la sensibilité des économistes par les émotions esthétiques que les modèles mathématiques produisent. Nous mettons tout d’abord en évidence que, dans le champ des mathématiques, de nombreux chercheurs adhèrent à l’idée que la beauté esthétique d’une théorie est révélatrice de la « vérité » qu’elle incarne : les émotions esthétiques ont, en ce sens, une fonction épistémique qui permet de connaître ou d’approcher le réel. Nous montrons ensuite que la majorité des économistes qui ont construit la science économique dominante au cours du XXe siècle ont bien été sensibles à l’attrait esthétique des mathématiques, mais que cela s’est fait au détriment du réalisme des hypothèses des théories économiques. Nous montrons enfin, au travers de la figure tutélaire de Gérard Debreu, prix « Nobel » d’économie en 1983, que l’histoire de l’économie mathématique (et de son modèle le plus célèbre, le modèle d’équilibre général) est celle de la transmission d’une forme considérée par de nombreux économistes comme étant non sensible – axée sur la rationalité et la rigueur – qu’une communauté scientifique a en fait, bien au contraire, intégrée et partagée sur une base esthétique affective.
Mots-clefs : émotion esthétique, économie mathématique, modèle d’équilibre général, Gérard Debreu.
Summary
This article discusses the epistemic role of aesthetic emotions in mathematical economics. We hypothesize that mathematical formalisation in economics has helped to shape the sensitivity of economists through the aesthetic emotions that mathematical models produce. First of all, we highlight that, in the field of mathematics, many researchers subscribe to the idea that the aesthetic beauty of a theory reveals the « truth » it embodies: aesthetic emotions have, in this sense, an epistemic function that allows them to know or approach reality. We then show that the majority of economists who built the dominant economics approach during the 20th century were indeed sensitive to the aesthetic appeal of mathematics, but that this was at the expense of the realism of the assumptions of economic theories. Finally, we show, through the tutelary figure of Gérard Debreu, Nobel Prize winner in economics in 1983, that the history of mathematical economics (and its most famous model, the general equilibrium model) is that of the transmission of a form considered by many economists to be non-sensitive – based on rationality and rigour – that a scientific community has in fact, quite the contrary, integrated and shared on an emotional aesthetic basis.
Keywords: aesthetic emotion, mathematical economics, general equilibrium model, Gérard Debreu.
Introduction
L’immunologiste et historien des sciences, Ludwig Fleck, est l’un des premiers auteurs à avoir pointé le rôle central de l’émotion dans l’édification de la science. Dans Genèse et développement d’un fait scientifique[1], publié en allemand 1934, l’auteur polonais identifie, bien avant la notion de paradigme rendue populaire par Thomas Kuhn[2], le fonctionnement de la science académique autour d’une « communauté de pensée » à partir de laquelle le savoir peut émerger. Ce collectif correspond à la communauté des personnes qui échangent des idées, interagissent intellectuellement et partagent des positions, des hypothèses ou des méthodes communes. Dans ce cadre, certaines émotions (comme la crainte, la surprise, la joie, l’inquiétude, etc.) jouent « en arrière-plan » et donnent accès à une « connaissance personnelle » que le philosophe Michael Polanyi[3] décrit comme « indicible », c’est-à-dire inaccessible et non consciente. Les émotions ont ainsi, au niveau individuel et collectif, une incidence sur la motivation de la recherche – comme c’est le cas de l’émerveillement, l’étonnement ou la curiosité – mais aussi une influence particulière sur l’activité même de la recherche au travers du choix des outils, des méthodes, des hypothèses ou des orientations épistémologiques[4]. Lorsque, en particulier, les chercheurs observent un phénomène ou une donnée qui contredit la vision conventionnelle dans leur domaine d’expertise, ils peuvent ressentir une confusion, une perturbation, une forme d’anxiété ou d’inconfort, qui les incite à restaurer leur état émotionnel en trouvant l’origine de l’anomalie responsable de la contradiction. Des émotions comme la crainte, la recherche de sécurité, mais aussi la surprise, initient le mouvement vers un changement possible de paradigme scientifique : « toute épistémologie a pour point de départ une inquiétude[5] » selon la formule brève et synthétique des historiens des sciences, Lorraine Daston et Peter Galison.
Cet article porte sur le rôle épistémique des émotions esthétiques en économie mathématique. L’argument principal que nous soutenons est que la formalisation mathématique en économie a contribué à façonner la sensibilité des économistes par les émotions esthétiques que les modèles mathématiques produisent. Nous mettons tout d’abord en évidence que, dans le champ de la physique et des mathématiques, de nombreux chercheurs adhèrent à l’idée que la beauté esthétique d’une théorie est révélatrice de la « vérité » qu’elle incarne : les émotions esthétiques ont, en ce sens, une fonction épistémique qui permet de connaître ou d’approcher le réel. Nous montrons ensuite que la majorité des économistes qui ont construit la science économique dominante au cours du XXe siècle ont bien été sensibles à l’attrait esthétique des mathématiques, mais que cela s’est fait au détriment du réalisme des hypothèses des théories économiques. Nous montrons enfin, au travers de la figure tutélaire de Gérard Debreu, prix « Nobel » d’économie en 1983, que l’histoire de l’économie mathématique (et de son modèle le plus célèbre, le modèle d’équilibre général) est celle de la transmission d’une forme considérée par de nombreux économistes comme étant non sensible – axée sur la rationalité et la rigueur – qu’une communauté scientifique a en fait, bien au contraire, intégrée et partagée sur une base esthétique affective.
Que révèle la beauté des théories scientifiques ?
La conception de la beauté en science repose en partie sur des émotions que l’on qualifie d’ « esthétiques ». En psychologie, les émotions esthétiques résultent d’un jugement ou d’une appréciation portant sur la beauté de la nature, d’un paysage, d’un tableau ou sur les qualités intrinsèques d’une forme architecturale[6] ou d’une performance artistique[7]. Des émotions comme le ravissement, la félicité, la solennité, l’admiration, la fascination ou même l’extase, entrent dans cette catégorie d’affects distincte dans laquelle l’émotion n’est pas suscitée par une visée fonctionnelle ou adaptative. Pour autant, le sentiment esthétique peut avoir un impact sur la façon dont procède la science au travers de la façon dont est appréciée, plus ou moins consciemment, la « beauté » d’une théorie. Le caractère esthétique d’une théorie – sa beauté – dépend naturellement d’une appréciation personnelle, intime, subjective, mais aussi – si l’on suit la logique du « collectif de pensée » envisagée par Ludwig Fleck – sur la façon dont les chercheurs s’accordent sur les critères qui fondent la qualité ou l’opérationnalité d’une théorie. Chaque individu forme ainsi son jugement esthétique d’une manière qui est conforme à la communauté scientifique à laquelle il appartient.
Une question centrale concernant l’esthétisme en science est d’apprécier dans quelle mesure la beauté d’une théorie est révélatrice (ou non) de la vérité qu’elle incarne ? Une théorie est-elle belle parce qu’elle est « vraie » ? Ou, au contraire, est-elle considérée comme véridique en raison de ses propriétés esthétiques ? D’après le prix Nobel de physique américain, Steven Weinberg, l’esthétique confèrerait à la théorie un gage de scientificité dans la mesure où elle serait le signe que la recherche progresse « vers une théorie fondamentale ultime[8] ». Le mathématicien et physicien britannique, Paul Dirac (1902-1984), aimait à dire qu’il était plus important d’avoir une belle équation qu’une équation en accord avec l’expérience. Selon le philosophe et historien des sciences James McAllister[9], cependant, des formes ou des styles de théories qui se sont révélées empiriquement performantes dans le passé ont vocation, via un processus d’induction, à être valorisées sur le plan esthétique. Si, par exemple, un style de démonstration se révèle fructueux, alors il acquiert une valeur esthétique positive. Plus généralement, lorsqu’une théorie se révèle en accord avec l’expérience, ses propriétés esthétiques sont dès lors investies d’une valeur de vérité. La corrélation entre une propriété esthétique et une vérité scientifique, au sens ici de son adéquation avec l’expérience, n’est cependant jamais définitive. Par exemple, au XVIIIe siècle, en mécanique, une théorie était jugée d’autant plus belle qu’elle était abstraite. Au siècle suivant, une belle théorie était davantage celle qui permettait de visualiser des phénomènes. Ceci signifie que les préférences esthétiques d’une communauté scientifique sont naturellement sujettes à une forme d’inertie ou de conservatisme mais qu’elles peuvent évoluer dans le temps. James McAllister rappelle par exemple, que la motivation centrale d’Albert Einstein n’était pas d’élaborer une théorie empiriquement plus performante, mais de se débarrasser, sur la base d’un critère esthétique, des asymétries qui apparaissaient en appliquant, dans le champ de la mécanique newtonienne, les équations fondamentales de Maxwell à des corps en mouvement[10].
Les émotions esthétiques ont donc une incidence sur la façon dont se construit un corpus scientifique : (i) elles en sont un révélateur, a posteriori, les théories empiriques adéquates étant perçues au fil du temps comme les plus belles ; (ii) elles en sont également l’un des moteurs lorsque les chercheurs modifient leurs préférences esthétiques pour s’engager dans d’autres styles de théories.
Depuis Platon, Aristote, Galilée, Newton, Leibnitz, jusqu’aux plus grand mathématiciens du XXe siècle, nombreux sont ceux qui, comme Henri Poincaré, considèrent que la beauté des mathématiques correspond à un réel sentiment esthétique que tous les « vrais » mathématiciens sont censés reconnaître. Le processus de découverte en mathématiques est souvent long, fastidieux, ardu. Mais il laisse aussi une place à une forme d’ « intuition », à un moment de « vérité » (« Eurêka ! »), de déclic, sur lesquels les mathématiciens s’expriment volontiers[11]. Gian-Carlo Rota voit dans cette phase d’ « illumination », qui contient aussi, de son point de vue, une part d’illusion, l’un des éléments qui confèrent à la discipline une forme de beauté[12]. Comme dans de nombreuses disciplines, et en particulier, en mathématiques, les émotions implicites ou inconscientes qui contribuent au processus de découverte et à la construction de la théorie sont souvent masquées par le fait que les résultats s’expriment de façon concise, formelle, logique, effaçant les traces de leur genèse. Une fois le travail de création accompli, le chercheur, et sa communauté, rationalise et schématise le chemin qui a conduit au résultat, évacuant en partie les effets du hasard et des affects diffus qui ont participé à la recherche. Selon la jolie formule de Thomas Kuhn, « contrairement à l’art, la science détruit son passé[13] ».
Dans le langage des mathématiciens aujourd’hui, les qualités esthétiques d’une preuve formelle sont synonymes de « beauté », d’ « harmonie », d’ « élégance », de « profondeur », d’ « inspiration », d’ « étonnement » ou encore d’ « ingéniosité »[14]. Ces qualités correspondent à certains critères jugés pertinents dans la discipline, comme la symétrie, la clarté, la concision, la rigueur, la simplicité, la cohérence ou la complétude. On se rappelle par exemple que Paul Dirac ajoute en 1928 un terme à l’équation qui porte son nom par souci de symétrie, par une intuition que cette symétrie a un sens dans la description des particules élémentaires, ce qui sera justifié plus tard sur le plan expérimental. Les sciences mathématiques, nous dit Aristote, « mettent en évidence l’ordre, la symétrie et la limitation ; et cela ce sont les grandes formes de la beauté[15] ». La symétrie, concept éminemment central en architecture, dans le domaine artistique, mais aussi en psychologie des formes (le visage ou le corps), reflète pour le mathématicien, dans une acception dynamique, l’invariance d’une structure par rapport à des transformations auxquelles elle est soumise. Une mosaïque périodique (voir l’image ci-dessous[16]), par exemple, de même qu’une frise, est insensible à certaines translations. Le mathématicien George Birkhoff a lui-même proposé une mesure de l’esthétique de différents objets (considérée comme un rapport entre son niveau d’ordre et sa complexité) et calculé sa valeur numérique pour des formes géométriques diverses, des harmonies musicales ou même des poèmes[17]. L’ordre et la complexité sont décrites à partir de fonctions linéaires de plusieurs variables dans lesquelles figure notamment la symétrie horizontale et verticale de l’objet.
C’est sur la base de ces différents critères (clarté, cohérence, etc.) que l’équation d’Euler, eiπ + 1 = 0, peut légitiment revendiquer, le titre de la « plus belle formule mathématique ». Forme concise et simple, intégrant à la fois le zéro, l’unité arithmétique, le nombre e (nombre irrationnel qui est la base des logarithmes naturels) mais aussi l’unité imaginaire i ainsi que le célèbre nombre π, l’équation suscite une émotion esthétique qui naît « d’une parfaite adéquation entre la forme et la densité d’information qu’elle véhicule[18] ». Au sein d’une communauté scientifique, cela a donc du sens d’évoquer une « orientation émotionnelle[19] », décrivant notamment les préférences esthétiques partagées par les chercheurs dans un domaine. L’émotion esthétique, attribut individuel, est influencée par la reconnaissance, au sein de la communauté, de l’harmonie des critères de beauté qui caractérisent la discipline. Cette harmonie, nous dit Henri Poincaré, « est à la fois une satisfaction pour nos besoins esthétiques et une aide pour l’esprit, qu’elle soutient et qu’elle guide[20] ».
L’esthétisme de l’économie mathématique, un défi au réalisme ?
La science économique standard ou « dominante » a intégré, depuis le début du XXème siècle, les apports des mathématiques et leur rigueur, par l’intermédiaire notamment d’une tradition française qui va d’Augustin Cournot à Gérard Debreu ou Maurice Allais, en passant naturellement par son plus illustre fondateur, Léon Walras (1834-1910). Les économistes contemporains conçoivent depuis une véritable « fascination » pour cet outil noble et rigoureux. Ils bénéficient de la notoriété des mathématiques, son usage étant notamment considéré par beaucoup d’économistes comme un gage de scientificité et d’objectivité. En raison de l’adhésion majoritaire des économistes tout au long du siècle passé à une science économique standard basée sur la formalisation et l’axiomatique, on peut s’interroger sur la façon dont leur « admiration », parfois leur dévotion, a contribué à façonner leur culture scientifique. Les économistes mettent-ils en avant, eux aussi, l’élégance ou la parcimonie de leurs modèles comme un critère de sélection d’une théorie ? L’émotion esthétique, la beauté, est-elle considérée et reconnue ? Les critères esthétiques abstraits induits par le recours à la formalisation et dérivés des mathématiques (complétude, symétrie, rigueur, cohérence, simplicité, etc.) sont-ils porteurs d’un critère de « vérité » en économie ? Ont-ils en ce sens une portée épistémique ?
Le spécialiste de l’histoire de la pensée économique, Mark Blaug, a décrit la spécificité de ce qu’il a appelé la « révolution formelle[21] » qui touche la science économique au tournant des années 1950. Dès le début du XXe siècle, dans la continuité de la « Révolution Marginaliste » (1871-1874), et dans la lignée de l’ingénieur-économiste Léon Walras, l’analyse économique se tourne résolument vers l’utilisation des mathématiques. Jules Dupuit, Augustin Cournot, Alfred Marshall, Francis Edgeworth, puis, plus tard, l’économiste américain Paul Samuelson, incarnent cette mouvance de chercheurs qui plébiscitent leur usage renforcé dans la construction de la théorie économique. Léon Walras avait cependant à l’esprit, comme la plupart de ses successeurs, que l’usage des mathématiques devait servir un objectif précis : la description et la représentation des mécanismes réels à l’œuvre en économie. Walras adhérait sans doute à la croyance (platonicienne) que le sens donné à la structure des mathématiques était similaire à celui contenu dans la structure de l’économie. Le modèle d’équilibre général de Walras est ainsi rentré dans l’histoire comme une représentation quasi-réaliste, à partir d’un système d’équations, d’une économie de marché. Le modèle pose notamment certaines questions concrètes centrales : en quoi l’interdépendance entre les marchés des biens et des services modifie-t-elle la dynamique des prix d’équilibre ? La détermination du système des prix peut-elle être centralisée ou est-elle le fruit de la coordination involontaire des agents économiques ?
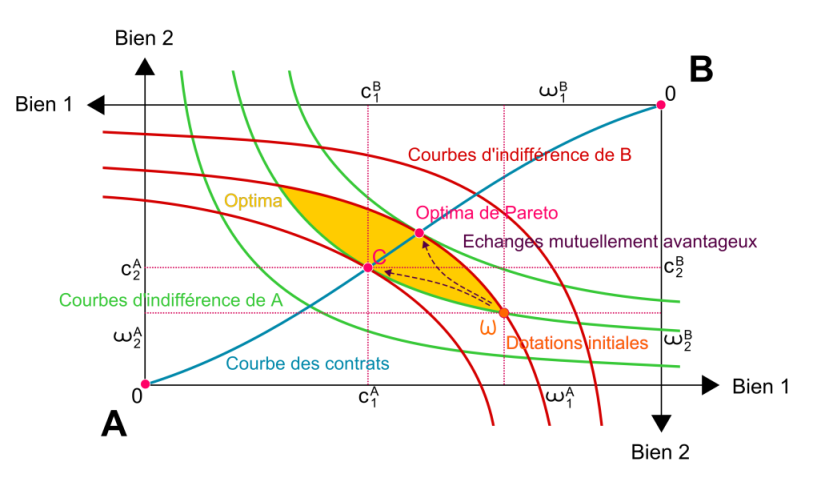
Selon Mark Blaug, cette conception initiale, instrumentale et appliquée, de l’approche mathématique walrasienne, se distingue de celle illustrée, au moment de la « révolution formelle » symbolisée par le modèle d’Arrow-Debreu[22] publié en 1954. Le modèle propose une analyse « axiomatique » de l’équilibre général en se basant sur une méthode topologique (spatiale ou géométrique) plutôt que sur le calcul d’équations. En utilisant une méthode de preuve mathématique indirecte, à partir du « théorème du point fixe », il montre l’existence d’un vecteur de prix d’équilibre dans une économie concurrentielle idéale décentralisée. La pierre angulaire de l’économie mathématique, le modèle d’Arrow-Debreu, pour lequel le mathématicien Gérard Debreu a été honoré (à sa grande surprise et, possiblement, pour son grand désarroi) du Prix de la Banque de Suède en sciences économiques en mémoire d’Alfred Nobel en 1983, a été célébré dans la communauté des économistes-mathématiciens qui ont, dans leur grande majorité, été séduits par son caractère épuré et par son élégance. Le modèle a fait naître une tradition d’économie mathématique et a imprégné une très grande partie des contributions des économistes contemporains, bien au-delà de l’équilibre général. Cette tradition repose en partie sur le plaisir esthétique attribué à la formalisation économique. Paul Samuelson a, en particulier, souligné la beauté de la théorie de David Ricardo (le principe de l’avantage comparatif en commerce international) dont il proposera une extension formelle à partir de l’équilibre général[23]. L’économiste américain Frank Hahn a évoqué le « frisson de plaisir » qu’il éprouvait à la lecture du « théorème du cœur » spécifique d’une économie d’échanges[24] : la « boîte d’Edgeworth », proposée par Francis Edgeworth[25] et perfectionnée par Vilfredo Pareto, est en effet une illustration convaincante du caractère très séduisant de la construction géométrique et mathématique appliquée à la sphère de l’échange. La boîte présentée ci-dessous[26] illustre les possibilités d’échange de deux biens entre deux individus (A et B). Elle est utilisée pour représenter l’équilibre général dans une économie d’échange et permet de visualiser l’un des résultats les plus importants de l’économie du bien-être. Les courbes en vert et en rouge correspondent à ce que l’on appelle les « courbes d’indifférence » des individus, qui permettent de représenter leurs niveaux de préférence pour les biens (1 et 2) qui leur sont proposés sur le marché. La courbe dite des « contrats » correspond à l’ensemble des lieux d’échange qui sont profitables (avantageux) pour les individus (les optima de Pareto) : ils sont obtenus, en partant des dotations initiales en biens de chaque individu, et indiquent, c’est ce que montre le graphique, les points de tangence des courbes d’indifférence de A et de B. Un équilibre général est donc aussi un optimum (de Pareto) au sens où il impossible d’augmenter la satisfaction d’un individu (A par exemple) sans diminuer celle de l’autre (B). L’élégance et la beauté de cette construction provient tout d’abord de la courbure des fonctions d’indifférence (issue de leur convexité et de leur continuité dans l’espace), de la représentation figurative et claire du « cœur de l’échange » (au centre) et, sans doute, de l’extraordinaire symétrie de la boîte. Ce graphique ingénieux, dont la portée est grande, présente un caractère esthétique apparent du fait de sa capacité à décrire, avec fluidité, et dans un monde géométriquement clos, l’espace de l’échange. L’analyse est rigoureuse, précise, claire, cohérente et parcimonieuse (le modèle utilisant un nombre d’hypothèses réduit) : tous ces éléments sont les critères d’appréciation et d’évaluation de la qualité et de la beauté d’une théorie valorisés sur le plan scientifique par les économistes-mathématiciens.
Les critères esthétiques de rigueur, de complétude, de symétrie et de clarté d’exposition, mis en valeur par les économistes-mathématiciens dans le modèle d’Arrow-Debreu négligent cependant un autre critère d’évaluation pertinent pour une théorie : le réalisme de ses postulats. Le décalage entre la rigueur du modèle théorique d’Arrow-Debreu et sa déconnection par rapport au monde réel qu’il représente, atteste, selon Mark Blaug, de la force de la révolution formelle des années 1950. L’historien Till Düppe raconte notamment combien l’élaboration du modèle et son écriture furent l’objet d’un compromis incessant entre deux figures majeures de l’économie mathématique, l’éclectique et extraverti Kenneth Arrow et le plus austère et silencieux Gérard Debreu. Pour Kenneth Arrow, la preuve mathématique d’existence d’un équilibre général doit donner la priorité ou, au moins préserver, la signification économique du modèle. Pour Gérard Debreu, pur mathématicien élevé dans la tradition du « bourbakisme » (courant de pensée qui propose d’unifier les mathématiques au sein de la théorie des ensembles), il faut au contraire séparer la démonstration formelle de ses implications et de son interprétation. Dès lors, le modèle n’a nul besoin d’être en lien avec la réalité des mécanismes économiques qu’il est censé décrire. Les biens et les services sont par exemple représentés sous la forme la plus générale possible comme des objets mathématiques, en tant qu’ « éléments » appartenant à un « espace des biens » . Les termes de « joueur » ou de « stratégie » suggérés par Arrow sont remplacés par ceux plus neutres d’ « agent » ou d’ « action ». De l’aveu même d’Arrow, la version finale du papier est plus proche de celle désirée par son co-auteur que de la sienne. Pour Debreu, il s’agit toutefois encore d’un compromis qui le conduira, quelques années plus tard, à finaliser un travail plus abouti et plus conforme à ses objectifs initiaux dans la Théorie de la valeur[27] publiée en 1959. Sa réception, au sein de la communauté des économistes, est plus réservée. L’économiste d’origine russe Leonid Hurwitz la considère comme unique dans sa volonté de préserver la clarté et la rigueur de l’axiomatique au mépris d’autres objectifs utiles de modélisation[28]. L’américain Martin Shubik, l’une des figures marquantes de la théorie des jeux, en conclura que la rigueur est une « condition nécessaire mais non suffisante » pour qu’une contribution en économique mathématique constitue un apport significatif à l’analyse économique[29]. L’excès de rigueur et de formalisme limite la portée de ce que les économistes sont capables de dire sur le réel à partir de leurs modèles. Les hypothèses d’optimisation individuelle, de parfaite rationalité et de concurrence pure sont ainsi connues pour avoir été intégrées en partie en raison de leur simplicité et de leur grande compatibilité avec l’analyse mathématique. Elles ont cependant largement été critiquées depuis les années 1950 pour leur irréalisme : la rationalité humaine est « limitée[30] », l’erreur de jugement fréquente[31].
En dépit de critiques réitérées, à l’intérieur de son domaine mais aussi en provenance d’approches plus hétérodoxes, l’apport de Debreu a eu une influence très postérieure à la publication de ses travaux ou même à celle de l’attribution du prix Nobel en 1983. Il est ainsi probable que la connexion entre les mathématiques formelles et l’analyse économique a constitué un rempart contre les ouvertures potentielles, aujourd’hui revendiquées par l’économie comportementale[32], de la discipline en direction de la psychologie ou d’autres sciences sociales. Les mathématiques constituent encore aujourd’hui le langage principal à partir duquel sont véhiculées les propositions des économistes. Elles apportent concision, rigueur, clarté d’exposition, simplicité, profondeur et parcimonie à une discipline qui, à partir d’une conception rationnelle et égoïste de l’individu, prétend à une forme de généralité et d’universalité. Il peut ainsi apparaître paradoxal que dans une discipline qui a longtemps ignoré le rôle des émotions dans l’activité qu’elle décrit[33], favorisant a contrario la puissance de la rationalité pure, la fascination esthétique pour les mathématiques ait façonné la sensibilité des économistes via les émotions esthétiques que les modèles formels produisent.
De l’intime à la communauté : la transmission d’une forme (non) sensible
Il serait excessif d’attribuer à Gérard Debreu toute la responsabilité de la distance prise par l’économie mathématique vis-à-vis du réel. Il faudrait d’ailleurs, sans doute, mettre en perspective l’apport du formalisme et ses mérites dans la construction de la discipline. La question que nous posons pour finir est cependant de savoir quel est le poids de la personnalité de Gérard Debreu dans la diffusion de cette culture de la rigueur en économie. Dans quelle mesure, en particulier, l’outil scientifique, matérialisé ici par le modèle d’Arrow-Debreu, se construit-il à l’image de la personnalité ou des goûts esthétiques de son fondateur ? Dans quelle mesure, autrement dit, les émotions individuelles d’un chercheur peuvent-elles être transmises, via des concepts théoriques, et sans qu’il en ait pleinement conscience, à une communauté scientifique qui en reconnait le caractère esthétique ?
À la suite de l’obtention de son prix Nobel, Gérard Debreu a été conduit à s’exprimer, lors de sa déclaration à cette occasion puis, plus tard, dans un article dédié à cette question[34], sur sa conception de l’utilité des mathématiques dans l’analyse économique. Debreu insiste sur certains avantages liés au recours des mathématiques – la clarté d’expression, la capacité de généralisation, la limitation des hypothèses, l’affranchissement de l’idéologie – qui appuieront le discours récurrent des économistes-mathématiciens. Debreu insiste surtout sur sa croyance en l’utilité d’une séparation entre la preuve formelle et le contenu interprétatif du modèle. Au fur et à mesure qu’un modèle économique acquiert une « vie mathématique propre », il devient l’objet d’un processus inexorable dans lequel la rigueur, la généralité et la simplicité sont recherchés sans répit[35]. Une théorie économique devrait, selon lui, passer un « test acide » qui la débarrasserait de toute forme d’interprétation économique et qui ferait apparaître en l’état l’infrastructure mathématique sur laquelle elle repose. En suivant l’analogie proposée par Till Düppe[36], le test acide permet d’évincer le « corps » de la théorie (sa signification) au profit de son « squelette », et la rend en conséquence insensible à son environnement, immunisée contre la critique et, pouvons-nous ajouter, contre la réfutation. « Une théorie axiomatisée peut avoir une vie, mais une vie sans affection – comme un squelette hantant la science économique depuis 1959[37] ».
Dans le discours de Gérard Debreu, on trouve une tentative de justification de l’ascétisme de son travail formel. Cette clarification a été très largement rendue nécessaire par sa difficulté (son malaise) à expliciter pour quelle raison le modèle d’Arrow-Debreu ne peut avoir l’interprétation commune qu’on lui a prêtée et que le comité Nobel qui lui a attribué le prix a lui-même renforcée, à savoir l’idée selon laquelle les marchés s’auto régulent et sont, en conséquence, efficaces. Till Düppe y voit également une façon de s’ « excuser », empreinte de culpabilité, pour expliciter que telle n’était pas son intention dans l’édification de ce modèle et de sa preuve d’existence[38]. Dans le théorème qui porte son nom, dit de « Sonnenschein-Mantel-Debreu », établi au début des années 1970, Debreu et ses coauteurs montreront que l’on ne peut extraire de ce modèle autre chose qu’une condition d’existence de l’équilibre. Autrement dit, son unicité et la dynamique des prix vers l’équilibre – ce que Léon Walras appelait le « tâtonnement » – ne sont pas acquises. Le modèle est, de ce point de vue, vide d’interprétation, comme le suggérait initialement Debreu, puisque rien ne garantit qu’un équilibre de marché puisse converger sous la pression concurrentielle. Un « empereur sans habits » ironisera Alan Kirman[39]. Le théorème aurait pu – aurait dû selon Mark Blaug – sonner le glas de la théorie de l’équilibre général. Tel ne fut cependant pas le cas.
Debreu adhérait, on le sait, à la « beauté austère des mathématiques[40] ». Il entra sans conviction, comme le rappelle Till Düppe[41], dans l’univers des économistes. Il appartenait à l’école « bourbakiste » pour laquelle il avait une véritable fascination et qui correspondait pleinement à ses aspirations intellectuelles de rigueur et d’esthétique. À son image, comme l’a commenté Debreu lui-même, celle-ci véhiculait une tradition de grande réserve vis-à-vis de l’expression des sentiments, tradition tout à fait conforme à l’épistémologie de son temps[42]. Cet univers lui convenait parfaitement. Comme l’a évoqué son entourage – sa fille, son épouse, mais aussi ses amis et ses collègues – Gérard Debreu possède une personnalité mystérieuse, secrète, discrète, inquiète et silencieuse. Lors de la célébration de son soixante-huitième anniversaire, son collègue Dieter Sondermann lève un toast en son honneur et rappelle combien « Gérard a toujours été un modèle de perfection, qui non seulement parlait de la rationalité mais qui l’appliquait pour améliorer sa vie de tous les jours[43] ». Il ressentait, nous rapporte sa fille, Chantal Debreu, « une inquiétude sur sa capacité de contrôle et sur la possibilité d’une absence de contrôle » parce qu’un certain « nombre d’évènements dramatiques étaient survenus au cours de sa vie[44] ». Gérard Debreu incarne une aspiration au secret, à la perfection, à la rigueur, à la rationalité, qui à la fois a contribué à l’admiration que ses collègues lui ont porté au cours de sa carrière, et, sans doute, à l’isolement dont il a pu souffrir. L’univers des mathématiques axiomatiques était ce à quoi il aspirait et ce qui lui permettait aussi de se cacher pour éviter d’avoir à exprimer ses sentiments. En ce sens, son modèle de 1954, construit en collaboration avec Kenneth Arrow, incarne une forme esthétique pure, idéale, rationnelle, dénué apparemment d’affects, qui est aussi celle qui symbolise la personne et la vie secrète de Gérard Debreu. La conception de Gérard Debreu de ce que doit être un modèle économique repose donc sur une rationalité scientifique qu’il croit dénuée d’affect alors qu’elle repose en fait sur des émotions esthétiques spécifiques et sur la fascination véhiculée par les mathématiques. En proposant ce modèle d’économie pure, c’est un peu de cette forme-là – rationnelle, (non) sensible, rigoureuse – que Gérard Debreu a transmis, à son corps défendant, à la communauté des économistes.
L’on sait que la figure emblématique et historique de l’économie mathématique, Léon Walras, avait conscience de « planter un chêne », à l’ombre duquel ses successeurs pourraient élaborer une économie politique pure ayant vocation à devenir une science exacte. Walras a combattu ardemment et avec succès les critiques de ceux considérant que « la liberté humaine ne se laisse pas mettre en équation ». « La mathématique seule peut nous apprendre » nous dit-il en convoquant le jugement des mathématiciens[45]. En important les mathématiques au sein de l’économie politique, Walras a non seulement tenté un rapprochement avec les sciences naturelles, il a de fait ouvert la voie à un raffinement axiomatique et esthétique que ses successeurs, à l’instar de Gérard Debreu, ont incarné complètement. L’histoire de l’économie mathématique est aussi, au travers du modèle d’équilibre général, l’histoire d’une transmission d’une forme considérée par beaucoup économistes comme étant non sensible – axée sur la rationalité et la rigueur – qu’une communauté scientifique a en fait, bien au contraire, plus ou moins consciemment, intégrée et partagée sur une base esthétique affective.
[1] Ludwig Fleck. Genèse et développement d’un fait scientifique. Paris, Flammarion, 2008.
[2] Kuhn Thomas. La structure des révolutions scientifiques. Paris, Flammarion, 1983.
[3] Michael Polanyi. Personal knowledge: Towards a post-critical philosophy. University of Chicago Press, 2012.
[4] Emmanuel Petit. « Le rôle des émotions dans la pratique de l’activité scientifique », Cahiers Art et science, « Langage, Vérité, Exactitude », 2017, n°9.
[5] Lorraine Daston et Peter Galison. Objectivité, Paris, Presses du Réel, 2012, p. 429.
[6] Estelle Thibault. La géométrie des émotions: les esthétiques scientifiques de l’architecture en France, 1860-1950. Editions Mardaga, 2010.
[7] Klaus Scherer. « What are emotions? And how can they be measured? », Social Science Information, 2005, vol. 44.
[8] Steven Weinberg. Le rêve d’une théorie ultime. Paris, Odile Jacob, 1997.
[9] James W. McAllister. « Is Beauty a Sign of Truth in Scientific Theories? Why are some new theories embraced as beautiful, others spurned as ugly? Progress in science may require that aesthetic ideals themselves change », American Scientist, 1998, vol. 86, n° 2.
[10] Ibidem.
[11] Henri Poincaré. Science et méthode (1908). Kimé, 2011.
[12] Gian-Carlo Rota. « The phenomenology of mathematical beauty », Synthese, 1997, vol. 111, n° 2.
[13] Thomas Kuhn. La tension essentielle. Paris, Gallimard, 1990, p. 457.
[14] Matthew Inglis et Andrew Aberdein. « Beauty is not simplicity: an analysis of mathematicians’ proof appraisals », Philosophia Mathematica, 2014, vol. 23, n° 1.
[15] Cité dans Henri Volken. « Orientation émotionnelle mathématique : la raison esthétique », Revue Européenne des Sciences Sociales, n° XLVII-144, 2009, p. 122.
[16] https://fr.dreamstime.com/illustration-stock-configuration-de-mosa%C3%AFque-color%C3%A9e-abstraite-spectre-de-couleur-d-arc-en-ciel-fond-fleuri-multicolore-de-texture-vecteur-sans-image79348529
[17] George David Birkhoff. Aesthetic measure. Cambridge. Harvard, Harvard University Press, 1933.
[18] Henri Volken. « Orientation émotionnelle mathématique : la raison esthétique », op.cit., p. 123.
[19] Idem.
[20] Henri Poincaré. L’invention mathématique. In Cédric Villani, Les mathématiques sont la poésie des sciences, Flammarion, Champs, 2018, p. 107.
[21] Mark Blaug. « The formalist revolution of the 1950s », Journal of the History of Economic Thought, 2003, vol. 25, n° 2.
[22] Kenneth J. Arrow et Gérard Debreu. « Existence of an equilibrium for a competitive economy », Econometrica: Journal of the Econometric Society, 1954.
[23] Cassey Lee et Peter L. Lloyd « Beauty and the economist: the role of aesthetics in economic theory », Kyklos, 2005, vol. 58, n° 1.
[24] Frank Hahn. Money, growth, and stability. Cambridge, Mass.: MIT Press, 1985.
[25] Francis Ysidro Edgeworth. Mathematical psychics: An essay on the application of mathematics to the moral sciences. Kegan Paul, 1881.
[26] Source : https://upload.wikimedia.org/wikipedia/commons/3/30/Edgeworth_box.png (auteur : Cyrflo2000).
[27] Gérard Debreu. Théorie de la valeur. Dunod, Paris, 1959.
[28] Leonid Hurwicz. « ‘Review of Theory of Value.’ », American Economic Review, 1961, vol. 51, n°3.
[29] Martin Shubik. « ‘Review of Theory of Value.’ », The Canadian Journal of Economics and Political
Science, 1961, vol. 27, n°1.
[30] James G. March et Herbert A. Simon. « Cognitive limits on rationality », Organizations, 1958.
[31] Amos Tversky et Daniel Kahneman. « Judgment under uncertainty: Heuristics and biases ». Science, 1974, vol. 185, n° 4157.
[32] George Loewenstein. « Experimental economics from the vantage‐point of behavioural economics », The Economic Journal, 1999, vol. 109, n° 453.
[33] Emmanuel Petit. Économie des émotions. Paris, La Découverte, « Repères», 2015.
[34] Gérard Debreu. « The mathematization of economic theory », American Economic Review, 1991, vol. 81, n° 1.
[35] Gérard Debreu. « Theoretic models: mathematical form and economic content », dans George Feiwel (dir.) Joan Robinson and Modern Economic Theory. Palgrave Macmillan, London, 1989. p. 264-277.
[36] Till Düppe. « Debreu’s apologies for mathematical economics after 1983 ». Erasmus Journal for Philosophy and Economics, 2010, vol. 3, n° 1.
[37] Ibidem., p. 16 (notre traduction, nous soulignons).
[38] Idem.
[39] Alan Kirman. « The intrinsic limits of modern economic theory: the emperor has no clothes ». The Economic Journal, 1989, vol. 99, n° 395, p. 126-139.
[40] Gérard Debreu. « Random walk and life philosophy », The American Economist, 1991, vol. 35, n° 2, p. 3-7 (nous soulignons).
[41] Till Düppe. «Gérard Debreu‘s Secrecy: His Life in Order and Silence », History of Political Economy, 2012, vol. 44, n° 3.
[42] Lorraine Daston et Peter Galison. Objectivité, op.cit.
[43] Cité dans Till Düppe. « Gerard Debreu‘s Secrecy: His Life in Order and Silence », op.cit., p. 415 (notre traduction).
[44] Ibidem., p. 417 (notre traduction).
[45] Léon Walras. Études d’économie politique appliquée:(Théorie de la production de la richesse sociale). F. Rouge, 1898.
