Un jeune paradoxe : la Belle au bois dormant

  Laurent Delabre (Université Paris 1, IHPST)

L’énigme probabiliste de la Belle au bois dormant est un nouveau défi pour l’épistémologie formelle. Expliquer la nature de ce problème d’auto-localisation, chercher l’origine et les enjeux du vif débat qu’il suscite, mettre en relief le paradoxe redoutable qu’il engendre, résumer les principaux types de résolutions proposées dans la littérature et insister sur l’actuelle absence de consensus, sont les objectifs de cet article.

Dans l’expérience de la Belle au bois dormant, un agent au sommeil profond est réveillé soit une, soit deux fois, selon l’issue d’un tirage à pile ou face secret ; alors qu’il se trouve temporairement, à cause d’une drogue, dans l’incapacité de savoir s’il vit son premier ou un éventuel second réveil, il doit estimer rationnellement la probabilité que la pièce de monnaie soit tombée sur face, événement qui décide qu’il sera réveillé une seule fois durant l’expérience. Le problème engendre un paradoxe qui déchaîne les passions et mobilise des philosophes (philosophes analytiques et épistémologues pour la plupart), mais aussi des mathématiciens, voire quelques économistes et physiciens.

Née de diverses réflexions sur les mondes possibles, l’identité personnelle, ou encore les décisions d’un agent amnésique[1], l’énigme est popularisée en 2000 par le philosophe américain Adam Elga, auquel David Lewis, le théoricien des mondes centrés dont nous allons bientôt parler, répond l’année suivante[2], malheureusement quelques mois avant de décéder. Près d’une centaine de publications vont suivre. Cette incroyable effervescence, qui n’est pas terminée, est sans doute due à trois facteurs : le caractère inquiétant et clivant du paradoxe, sa portée pluridisciplinaire insoupçonnée et le développement d’Internet.

On dit que la Belle au bois dormant est un problème d’auto-localisation (self-location). Nous allons voir ce que cela signifie, juste avant d’en donner un énoncé complet. Ensuite, nous montrerons pourquoi il y a paradoxe et nous indiquerons de manière très succincte ce que les chercheurs ont jusqu’à présent proposé pour le démêler. Enfin, nous discuterons divers points, notamment l’utilité de ce puzzle probabiliste et la possibilité d’un consensus.

Auto-localisation

Ma mémoire est défaillante… Sommes-nous jeudi ou bien vendredi ? Quel est le sens d’une probabilité assignée à la proposition « on est jeudi » ? Nous pourrions répondre que l’explication par les mondes possibles, aujourd’hui répandue, suffit : quand je pèse « on est jeudi », j’estime une proportion, parmi tous les mondes possibles « proches » du nôtre qui me sont mentalement accessibles, de mondes où une contrepartie de moi-même se demande jeudi quel jour on est. Nous pouvons pourtant formuler une intéressante objection : ce type de propositions indexicales dont la valeur de vérité change au cours du temps ne peut pas se traduire en termes de mondes possibles. « Un monde où on est jeudi » n’a pas de sens, car jeudi est un moment et non un état du monde. En général, les croyances localisantes de se de type « je suis qui », « je suis où », « je suis quand » rechignent à se traduire en mondes, et l’attribution d’une probabilité devient problématique.

Inspiré par des travaux de W. V. O. Quine et de John Perry[3], David Lewis propose en 1979, dans son célèbre article Attitudes De Dicto and De Se, de considérer des parties temporelles d’un individu, qu’il appelle individuals-at-times ou plus simplement « centres », puis de penser des mondes centrés qui correspondront aux croyances de se quelles qu’elles soient et devraient permettre de mesurer ou de modifier leur degré aisément. Ainsi, un centre est un couple (S, t) où S est un sujet et t un instant ou un intervalle de temps. Un monde centré est un couple (c, m) où c est un centre et m un « classique » monde possible. « Le générateur a été branché ce matin et il est maintenant seize heures », c’est-à-dire « Je suis au temps seize heures dans un monde où le générateur est branché ce matin », c’est-à-dire « Moi-16 heures-générateur branché est actuel » est un exemple de proposition, dite proposition centrée, qui énonce une croyance d’auto-localisation.

Cependant, Lewis ne voit pas à cette époque que distribuer des probabilités sur des propositions centrées ou réviser ces probabilités en suivant des principes pourtant éprouvés tels que la conditionalisation bayésienne peut s’avérer très délicat dans certaines situations.

La Belle, un problème compartimenté

Dans les problèmes d’auto-localisation, un agent ou un groupe d’agents doit se repérer dans un lieu, un temps, un monde possibles, voire découvrir son identité, ou en tout cas peser des hypothèses localisantes. Les problèmes « compartimentés » en sont un sous-genre : l’agent vit une expérience où il sait qu’il est rendu partiellement amnésique à certains moments, si bien que, incapable de se situer précisément dans le temps, il a besoin d’estimer comme possiblement actuels un certain nombre de centres souvent colocalisés dans un même monde. Nous appellerons compartiment un monde centré (ou un ensemble de mondes centrés) que le sujet amnésique, à moins d’être (ré)informé, est incapable de reconnaître, de distinguer des autres mondes centrés pourtant disjoints que le protocole de l’expérience lui fait envisager avec probabilités non nulles. Si la définition n’est pas claire, un exemple sera le bienvenu, mais pas n’importe lequel : en effet, la Belle au bois dormant est devenue l’archétype des problèmes compartimentés. Voici un énoncé précis :

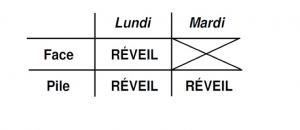
Ce dimanche soir, des chercheurs vont endormir pendant quelques jours la Belle au bois dormant ; puis ils lanceront une pièce de monnaie équilibrée. Selon le résultat, ils interrompront brièvement le sommeil de la Belle soit une, soit deux fois : si face, un réveil le lundi ; si pile, un réveil le lundi, un autre le mardi. Chaque fois, ils auront un entretien avec elle, puis la rendormiront à l’aide d’une drogue qui lui fera complètement oublier ce réveil. Voici que la Belle, qui connaît tout ce protocole, se réveille au cours de l’expérience, incapable de savoir si c’est lundi ou mardi. On lui demande alors : « À quel degré devez-vous croire que la pièce est tombée sur face ? » Que doit-elle répondre ?

Si certains chercheurs mettent ici un terme à l’énoncé, d’autres ont besoin, pour l’efficacité des démonstrations mais aussi afin de distinguer la résolution qu’ils proposent d’autres tentatives similaires, de le compléter ainsi : Si on est lundi, dès que la Belle a répondu à cette question principale, on lui annonce qu’on est lundi et on lui repose la question. Que doit-elle répondre alors ?

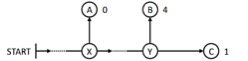
Nous comprenons que la Belle, une fois engagée dans l’expérience et réveillée, doit envisager au moins trois compartiments de type (BELLE, jour, orientation de la pièce) qui correspondent à trois réveils possibles : un réveil-face-lundi, un réveil-pile-lundi et un réveil-pile-mardi. La Belle reste inconsciente mardi en cas de face. Les trois compartiments se laissent aisément trouver dans ce schéma de l’expérience, qui résume les conséquences du tirage à pile ou face :

Un étrange écart entre deux probabilités

Une manière de goûter le paradoxe est de considérer les premiers raisonnements « naïfs » qu’à la place de la Belle nous pourrions tenir après un réveil dans l’expérience, avant une éventuelle annonce de la date :

• Dimanche soir, je croyais au degré 1/2 que la pièce, équilibrée, tomberait sur face. Mon présent réveil n’est pas une surprise, aucune information nouvelle ne m’autorise à préférer face ou à préférer pile. Donc je dois encore croire au degré 1/2 que la pièce est tombée sur face.
• Si l’expérience était répétée de très nombreuses fois, un réveil sur trois serait un réveil-face, donc la probabilité qu’un réveil particulier soit un réveil-face serait 1/3. Ainsi, même si la présente expérience n’a lieu qu’une fois, je dois croire au degré 1/3 que la pièce est tombée sur face.

Le premier raisonnement, typiquement bayésien, travaille une probabilité épistémique introduite dès le départ par alignement sur des chances objectives, en l’occurrence la propension de la pièce à tomber du côté face : quand la Belle se réveille dans l’expérience, elle maintient son degré de croyance en face du dimanche parce qu’elle respecte un principe d’inertie doxastique (pas d’information nouvelle pertinente, pas de révision des croyances). Le second raisonnement, fréquentiste, opte pour une « lecture ontologique fictionnelle » de la probabilité cherchée : la Belle se rappelle le protocole, imagine que l’expérience est répétée, que son réveil est un réveil parmi des milliers, et juge par conséquent qu’elle a deux fois plus de chances de vivre un réveil-pile ; elle ne conclut un degré de croyance, calqué sur la fréquence des réveils-face, que parce que la question de l’entretien l’exige. Le premier argument conclut 1/2, le second mène à 1/3. Le paradoxe est d’abord cette surprenante contradiction de deux conclusions : nous refusons la coexistence de deux réponses pourtant appuyées par des observations et des inférences en apparence simples et acceptables.

Mais nous devons regarder un peu plus loin : un écart peu ordinaire entre deux probabilités obtenues très différemment s’est creusé. Or, nous savons que l’interprétation de la probabilité est historiquement double (épistémique/ontologique) et, qu’un concept unique ait essentiellement un visage double ou que deux concepts soient à distinguer, nous pensons que des agents rationnels doivent craindre des divergences inexpliquées entre degrés de croyance et chances objectives. Nous comprenons donc que le paradoxe est une expression de la tension entre l’épistémique et l’ontologique et pouvons espérer que le résoudre dévoilerait un peu plus la nature de cet objet de recherche tardive qu’est la probabilité. D’ailleurs, en parcourant les publications sur la Belle depuis 2000, on observe une direction qui dépasse les acteurs particuliers du débat, une tendance à réparer la scission paradoxale en faisant de 1/2 une probabilité ontologique fréquentielle et plus seulement épistémique, ou bien en faisant de 1/3 une probabilité épistémique bayésienne et plus seulement ontologique.

La réponse 1/2 (à la question principale de l’entretien) est la plus intuitive chez la plupart des philosophes qui découvrent le problème. Cela s’explique en partie par une sympathie pour le principe d’inertie doxastique, même quand on n’avait jamais eu l’occasion de l’exprimer et de l’éprouver, en partie par la méfiance envers les simulations mentales éloignées des constats empiriques et envers ce comptage de réveils élémentaires qui fait fi de la dépendance des réveils-pile-lundi et des réveils-pile-mardi, événements qui arrivent nécessairement dans une expérience-pile. Pourtant, la réponse 1/3 est aujourd’hui majoritaire chez les chercheurs qui ont longuement participé au débat dans lequel, nous allons bientôt le voir, ne s’affrontent pas uniquement de simples pro-1/2 et pro-1/3.

Quatre résultats intuitifs aux conséquences absurdes

Présentons une autre manière d’apercevoir le paradoxe, complémentaire de la première. Elle est plus évoluée, requiert une bonne connaissance du débat, donc n’est pas cause de l’effet paradoxal qui accompagne la découverte du problème de la Belle. Cependant, elle ouvre assez naturellement la voie vers les grands types de résolutions du paradoxe rencontrés dans la littérature.

Avant de continuer, quelques conventions en très petit nombre s’imposent. Les questions de l’énoncé exigent des probabilités épistémiques, plus exactement des degrés rationnels de croyance, qu’on désigne souvent par des mots commençant par la lettre C : confiance, crédibilité, crédit (credence en anglais). Aussi, les trois mesures du crédit que la Belle accorde à ses croyances le dimanche, puis au moment où elle se réveille dans l’expérience, et enfin après l’annonce « on est lundi » seront notées respectivement : C_dim(.), C_rév(.) et C_lun(.). Ces distributions satisferont les axiomes de Kolmogorov[4]. Deux propositions non centrées et trois propositions centrées énonceront les principales croyances dont la Belle estime la probabilité :

F : « La pièce tombe sur face »

P : « La pièce tombe sur pile »

FL : « La pièce tombe sur face et on est lundi » i.e. « Je suis dans un réveil-face-lundi »

PL : « La pièce tombe sur pile et on est lundi » i.e. « Je suis dans un réveil-pile-lundi »

PM : « La pièce tombe sur pile et on est mardi » i.e. « Je suis dans un réveil-pile-mardi »

Remarquons que, pour tout sujet engagé dans l’expérience, FL, PL et PM sont exclusives et conjointement exhaustives (de même F et P) : à tout moment, la somme des probabilités associées à ces trois propositions est égale à 1. Voici d’autres égalités qui ne sont jamais remises en cause dans les débats :

• C_dim(F) = C_dim(P) = 1/2, valeur obtenue par alignement, le dimanche, sur la propension de la pièce équilibrée à tomber sur pile ou sur face (Principe Principal de Lewis).
• C_rév(PL) = C_rév(PM), en vertu d’un principe d’indifférence étendu aux croyances localisantes, plus exactement aux centres colocalisés dans le même monde possible.
• C_lun(FL) = C_lun(F), en vertu d’un principe d’équiprobabilité de propositions équivalentes étendu à des propositions centrées qui ne peuvent être équivalentes à d’autres propositions que dans un certain contexte (ici, FL et F ne sont équivalentes pour la Belle que durant l’expérience, où un réveil-face ne peut avoir lieu qu’un lundi).

Voici maintenant quatre résultats difficilement contestables au premier abord :

(1)    C_rév(F) = C_dim(F), par inertie doxastique entre dimanche et le réveil.

(2)    C_lun(F) = 1/2, par alignement sur les chances objectives le lundi (en apprenant qu’elle est réveillée lundi, événement qui devait assurément arriver, la Belle ne fait que récupérer ce que le protocole lui a temporairement pris ; plus rien d’important ne la distingue d’un individu extérieur à l’expérience qui aligne son degré de croyance en face sur la propension de la pièce à tomber sur face, tant que rien ne lui fait préférer un côté de la pièce plutôt que l’autre).

(3)    C_rév(FL) < C_lun(FL), par conditionalisation et vérification du « pouvoir confirmant » de l’information « on est lundi » = FL V PL (il suffit de poser le théorème de Bayes puis de transformer la formule pour faire ressortir l’inégalité des deux probabilités).

(4)    C_rév(FL) = C_rév(F), en vertu du principe étendu d’équiprobabilité de propositions équivalentes (voir plus haut).

Le souci est que l’on conclut de tout cela des contradictions, telles que C_rév(F) = C_lun(F) et C_rév(F)  < C_lun(F), voire des aberrations telles que C_rév(F) < C_rév(F) ! Certes, le paradoxe devrait être pleinement manifeste à présent, mais si nous considérons qu’un des quatre résultats précités est faux, nous entrevoyons des pistes de résolution. Il se trouve que les chercheurs se concentrent sur l’un ou sur l’autre de ces quatre résultats et n’explorent pas d’autres pistes.

Le tiérisme, ou les tiérismes

Si l’exposé qui précède ne vous a pas montré un paradoxe troublant mais stimulant, c’est peut-être parce que votre esprit est trop accaparé par une solution évidente à ses yeux. Le débat philosophique et la discussion des principes ne sont pas une lutte contre des vues résolument antagoniques, mais une attention dirigée vers un autre discours sensé et une recherche de négligences et d’erreurs dans sa propre argumentation, dans le but de construire une résolution meilleure. Rappeler cela, ce n’est pas réciter un sermon inutile ou déplacé : un paradoxe est fort parce que sa solution paraît simple, ce qui nous incite, malgré notre expérience, notre méthodologie et notre ouverture d’esprit, à sous-estimer les sons discordants. Accepter le témoignage des chercheurs sur l’actuelle absence de consensus, ce n’est pas reconnaître un échec de la raison, c’est se donner la chance de faire disparaître le paradoxe, plus tard, pour de bon. La suite de cet article ne donne qu’un faible aperçu du vaste débat en cours, qui part dans beaucoup de directions.

Commençons notre exploration par le refus du seul résultat (1) C_rév(F) = C_dim(F), remplacé par C_rév(F) = 1/3, positionnement communément appelé tiérisme[5] (thirdism) : effectivement, même s’ils répondent 1/2 à la question subsidiaire du lundi, les tiéristes répondent 1/3 à la question principale de l’entretien. Aujourd’hui coexistent en réalité au moins trois tiérismes, trois tentatives pour corriger l’argument adverse (qui utilise le principe d’inertie doxastique), voire lui substituer un meilleur raisonnement :

• Le tiérisme « bayésien » accepte la règle d’inertie doxastique mais pas son application dans le cas de la Belle, il considère en effet que cette dernière acquiert au moment de son réveil une information essentiellement indexicale (qu’elle ne peut exprimer qu’à l’aide d’un indexical, une fois engagée dans l’expérience) pertinente pour l’issue pile/face : « Je suis réveillée aujourd’hui »[6].
• Selon un autre tiérisme, qui souligne l’insuffisance de certaines théories bayésiennes et notamment la faiblesse du principe d’inertie doxastique, la Belle doit changer au réveil son degré de croyance en face même sans avoir reçu de nouvelle information, parce que sa localisation temporelle est devenue pertinente pour l’issue pile/face[7].
• Un autre tiérisme, qui « boit à plusieurs sources », affirme d’une part que l’argument adverse est soutenu au mépris de toute analyse fréquentiste, voire au mépris du réel, d’autre part que le fait que la Belle « existe en double » dans une expérience-pile, et qu’elle le sache, déforme son espace privé de probabilité (idée empruntée à certains raisonnements anthropiques)[8].

Demisme, double demisme et désambiguïsation

On peut accepter la relation (1) C_rév(F) = C_dim(F), c’est-à-dire C_rév(F) = 1/2, mais en revanche :

• contester le seul résultat (2) C_lun(F) = 1/2, lui préférer C_lun(F) = 2/3 et ainsi prendre parti pour le (simple) demisme (halfism), qui répond 1/2 seulement à la question principale de l’entretien. Il existe un demisme rare qui allie fréquentisme et bayésianisme, selon lequel les bons objets à compter lors d’une répétition de l’expérience sont justement des expériences, donc des groupes d’un ou de deux réveil(s). Mais le demisme le plus connu, le plus critiqué, si ce n’est décrié, est purement bayésien et justifie la contre-intuitive probabilité subjective 2/3, qui s’écarte des chances objectives, en considérant « on est lundi » comme une information inadmissible au sens lewisien[9].
• rejeter le seul résultat (3) C_rév(FL) < C_lun(FL) au profit de C_rév(FL) = C_lun(FL) et défendre ainsi un double demisme (qui répond 1/2 aux deux questions de l’entretien). Pour quelques doubles demistes, le principe de conditionalisation n’est tout simplement pas applicable au moment où la Belle, informée que c’est lundi, passe d’une situation où elle se localise dans une expérience datable à une situation où elle se repère plus précisément dans un jour datable[10]. D’autres doubles demistes cherchent une loi de révision doxastique concurrente de la conditionalisation, adaptée aux problèmes compartimentés et qui, après élimination d’un compartiment, ne grossirait que les probabilités associées aux compartiments voisins (centres différents mais même monde possible)[11].

Nous arrivons à une dernière piste. Appelons « désambiguïsation » toute tentative de résolution remplaçant d’une part le résultat (4) C_rév(FL) = C_rév(F) par C_rév(FL) = 1/3, et expliquant d’autre part que les réponses 1/2 et 1/3 que la Belle peut formuler au réveil (quand elle ignore la date) sont les réponses à deux questions distinctes que l’énoncé du problème mélange.

• Selon les désambiguïseurs (ou désambiguïsateurs) fréquentistes, 1/2 et 1/3 sont les probabilités de deux événements différents : se focaliser uniquement sur l’événement face en tant qu’issue possible du jet de la pièce, ou uniquement sur face en tant que réveil, c’est commettre l’erreur de mal examiner le dispositif aléatoire, l’organisation du réel[12].
• Pour les désambiguïseurs bayésiens, une proposition centrée et une autre non centrée, équivalentes dans un certain contexte, ne sont pas forcément équiprobables : FL et F sont crues avec la même intensité par qui se situe assurément lundi, pas par qui hésite entre deux dates. Cet ultime point de vue est très récent et très minoritaire ; à vrai dire, une seule publication le défend actuellement[13].

Des stratégies pour soutenir telle ou telle solution

Récapitulons les probabilités que les avocats des différentes positions précitées recommandent à la Belle lorsqu’elle doit répondre à la question…

                                   … principale    … subsidiaire (lundi)

        Tiérisme                       1/3                       1/2

       Demisme                       1/2                       2/3

 Double demisme                 1/2                       1/2

Désambiguïsation            1/2 et 1/3                 1/2

Nous avons montré que chaque position fait face à une difficulté majeure : le tiérisme doit expliquer pourquoi la Belle change son degré de croyance en face lorsqu’elle se réveille, et ce n’était pas une surprise, dans l’expérience ; le demisme doit justifier une insolite réponse 2/3 à la question subsidiaire ; le double demisme doit dire pourquoi la Belle conserve le degré 1/2 tout au long de l’entretien du lundi, où elle gagne pourtant une information ; la désambiguïsation doit expliquer pourquoi la Belle est autorisée à donner deux réponses à la question principale.

Pour contourner ces difficultés et délaisser quelque temps les discussions de fond, plusieurs chercheurs usent de stratégies diverses, de méthodes astucieuses pour faire ressortir une probabilité plutôt qu’une autre. Citons la classique analogie avec des urnes, l’analogie avec d’autres problèmes résolus ou non (Conducteur distrait, Argument de l’Apocalypse, Monty Hall…), l’appel aux interprétations de la mécanique quantique, l’élaboration de systèmes de paris hollandais (Dutch books), ou encore, évidemment, la variation du protocole. Abondantes, les variantes du scénario de la Belle sont parfois persuasives. Pourtant les auteurs doivent encore expliquer pourquoi l’analyse concluante d’une variante, qui généralement évacue une subtilité ou un obstacle, peut trancher le problème original.

Une stratégie n’est donc pas une résolution mais peut orienter une résolution du paradoxe. Cependant, elle mêle quelquefois la Belle à des théories scientifiques peu assurées (pensons aux controverses sur les interprétations de la mécanique quantique). Il arrive qu’elle pointe une zone d’ombre dans l’argumentation de fond qu’elle survole mais, souvent, elle en est inconsciente et reste biaisée. Cela rappelle l’erreur, plus grave encore, de quelques mathématiciens qui négligent les récentes réflexions philosophiques sur l’auto-localisation, réduisent sans justification l’aventure du sujet Belle à un croisement de simples événements aléatoires objectifs (pile ou face, lundi ou mardi) et croient calculer méthodiquement les bonnes probabilités avec des outils savants mais qui n’ont fait leur preuve qu’en s’appliquant à d’incontestables états possibles du monde. De même, il va sans dire que toute simulation informatique pour approcher une fréquence limite souffre immanquablement de biais en faveur du demisme ou au contraire du tiérisme, donc ne peut pas prétendre fournir une solution.

Les fruits de notre réflexion

La Belle au bois dormant est un paradoxe probabiliste aux qualités certaines. Notamment, nous avons signalé tout à l’heure qu’il interroge le concept double de probabilité. Les principes du bayésianisme comme ceux du fréquentisme sont revisités dans les analyses de la Belle ; d’après certains auteurs, ces deux approches sont même mises en grande difficulté. En outre, des concepts comme la conscience, le temps ou l’identité sont actualisés et affermis en tant qu’objets de recherche.

Les enjeux des débats sont donc nombreux, et ce n’est pas tout. Les problèmes d’auto-localisation compartimentés sont souvent associés ou confondus avec des problèmes de raisonnement anthropique dont l’examen doit nous apprendre à corriger des biais dans l’observation de notre mode d’existence et de notre environnement, et à affiner les probabilités de diverses conjectures scientifiques et philosophiques parfois insolites : apparition/disparition de l’homme sur Terre, immortalité de l’âme, vie extraterrestre et même hypermondaine (dans d’hypothétiques mondes parallèles) ou altermondaine (dans des mondes possibles qui auraient une existence autre que logique, qui auraient le même statut ontologique que notre monde), etc. Un scénario comme la Belle semble simple, concret, il ignore de prime abord toute métaphysique : il est pratique car il déplace en terrain connu des problèmes qui font appel à des démiurges ou à des mondes étrangers. Ajoutons qu’il y a des implications morales à toutes ces réflexions.

Les tiéristes sont parfois très confiants. Il est vrai qu’ils sont majoritaires et que peu d’entre eux modifient leur point de vue, alors qu’il est moins rare de voir des demistes évoluer vers le tiérisme, voire vers la désambiguïsation. Mais être pro-1/3, c’est soutenir une probabilité, pas proposer à la communauté des chercheurs un unique raisonnement afin que sa validité soit éprouvée. Les tiéristes sont encore très divisés. Que penser d’une solution expliquant la chute d’une probabilité de 1/2 à 1/3 par un gain d’information, et une autre l’expliquant par une perte de repère temporel ? Elles semblent résolument opposées ! En outre, beaucoup de « tiéristes » n’apportent que des stratégies faisant préférer la solution 1/3, mais n’épousent explicitement aucun courant tiériste particulier et n’affrontent pas les arguments parfois très poussés de leurs contradicteurs. Dans ces conditions, il est aujourd’hui trop tôt pour prétendre que le débat va prendre fin avec une entente sur tel raisonnement précis.

La mauvaise nouvelle, c’est donc que nous sommes encore loin d’un consensus. La bonne nouvelle, c’est que les recherches progressent, que le débat animé produit des idées neuves qui alimentent des débats connexes. Avec la Belle au bois dormant, nous vérifions encore une fois qu’un paradoxe ne nous mène jamais, après une agitation cérébrale vaine, dans une impasse, mais qu’il nous alerte, nous fortifie, nous prépare à de nouveaux défis.

Bibliographie sélective :

Bostrom, Nick

2007 Sleeping Beauty and Self-Location: A Hybrid Model, Synthese 157, 59-78

Bradley, Darren

2011 Self-location is No Problem for Conditionalization, Synthese 182, 393-411

Cozic, Mikaël

2007 Imaging and Sleeping Beauty: A Case for Double Halfers, dans D. Samet, Proceedings of TARK 2007 Conference, Presses Universitaires de Louvain, 112-117

Delabre, L. et Gerville-Réache, L.

2015 Insaisissable Belle au bois dormant, Philosophia Scientiae 19(1), 251-269.

Delahaye, Jean-Paul

2003 La Belle au bois dormant, la fin du monde et les extraterrestres, Pour la Science 309, 98-103

Elga, Adam

2000 Self-Locating Belief and the Sleeping Beauty Problem, Analysis 60, 143-147

Groisman, Berry

2008 The End of Sleeping Beauty’s Nightmare, The British Journal for the Philosophy of Science 59, 409-416

Horgan, Terry

2004 Sleeping Beauty Awakened: New Odds at the Dawn of the New Day, Analysis 64, 10-21

Lewis, David

1979 Attitudes De Dicto and De Se, The Philosophical Review 88, 513-543

2001 Sleeping Beauty: Reply to Elga, Analysis 61, 171-176

Lewis, Peter

2010 Credence and self-location, Synthese 175, 369-382

Perry, John

1979 The Problem of the Essential Indexical, Nous 13, 3-21

Piccione, M. et Rubinstein, A.

1997 On the Interpretation of Decision Problems with Imperfect Recall, Games and Economic Behavior 20, 3-24

Quine, W. V. O.

1969 Propositional Objects, dans Ontological Relativity and Other Essays, Columbia University Press, 139-160